Un homme ayant perdu ses clés dans la nuit, les cherche de réverbère en réverbère. Il arrive au dernier… Il ne sait pas si c’est l’endroit où il les a perdues mais c’est le seul lieu éclairé de la rue qu’il n’a pas encore visité…

En persévérant, l’individu progresse dans sa recherche. A-t-il pour autant plus de chances de trouver ses clés lors de cette ultime tentative qu’il n’en avait à la première ? Nous avons tendance à chercher des solutions là où il est facile de chercher et de persévérer, mais cela est-il vraiment pertinent ?
Ce n’est pas évident.
Plus il y a de tentatives infructueuses, plus les chances de trouver les clés sous un lampadaire sont faibles : il y a en effet plus de chances de les trouver sous un des lampadaires ![]() que parmi les lampadaires
que parmi les lampadaires ![]() . En même temps, il y a plus de chances de ne pas les trouver sous les
. En même temps, il y a plus de chances de ne pas les trouver sous les ![]() premiers lampadaires que sous les
premiers lampadaires que sous les ![]() premiers.
premiers.
Alors, lequel des deux effets va l’emporter ?
C’est le premier paradoxe du lampadaire. À chaque étape la probabilité ![]() que les clés soient sous un autre lampadaire, sachant qu’elles n’étaient pas sous les premiers, diminue avec le nombre de tentatives
que les clés soient sous un autre lampadaire, sachant qu’elles n’étaient pas sous les premiers, diminue avec le nombre de tentatives ![]() . Cependant la probabilité
. Cependant la probabilité ![]() , de les trouver à chaque nouveau lampadaire, sachant qu’elles n’étaient pas sous les précédents, est toujours plus grande qu’au départ…
, de les trouver à chaque nouveau lampadaire, sachant qu’elles n’étaient pas sous les précédents, est toujours plus grande qu’au départ…
Comment raisonner ? Globalement, les ![]() lampadaires éclairent une certaine proportion
lampadaires éclairent une certaine proportion ![]() de la rue. Pour nous,
de la rue. Pour nous, ![]() est donc un nombre connu strictement compris entre 0 et 1 exprimant tout simplement la probabilité que les clés soient éclairées.
est donc un nombre connu strictement compris entre 0 et 1 exprimant tout simplement la probabilité que les clés soient éclairées.
Tous les lampadaires ne sont pas équivalents, il y a plus de chances de trouver les clés à certains endroits plutôt qu’à d’autres. On note ![]() la part qui revient au réverbère
la part qui revient au réverbère ![]() . Autrement dit, la probabilité que les clés soient au pied du lampadaire
. Autrement dit, la probabilité que les clés soient au pied du lampadaire ![]() vaut :
vaut : ![]() . On suppose aussi que l’individu commence sa recherche par les endroits qui sont les plus probables, on suppose donc :
. On suppose aussi que l’individu commence sa recherche par les endroits qui sont les plus probables, on suppose donc :
![]()
![]()
On désigne enfin par ![]() la fonction de répartition associée à la distribution des
la fonction de répartition associée à la distribution des ![]() de la façon suivante :
de la façon suivante :
![]()
![]()
Dès lors, la probabilité ![]() que les clés soient sous un des
que les clés soient sous un des ![]() lampadaires restants sachant qu’elles n’étaient pas sous les
lampadaires restants sachant qu’elles n’étaient pas sous les ![]() premiers est donnée par :
premiers est donnée par :
![]()
![]()
On remarque effectivement que ![]() est une fonction décroissante de
est une fonction décroissante de ![]() . À chaque étape
. À chaque étape ![]() , la probabilité
, la probabilité ![]() que les clés soient sous un des lampadaires restants, sachant qu’elles n’étaient pas sous les
que les clés soient sous un des lampadaires restants, sachant qu’elles n’étaient pas sous les ![]() premiers, diminue bien avec
premiers, diminue bien avec ![]() .
.
Par ailleurs, savoir qu’il y a eu ![]() échecs avant la
échecs avant la ![]() -ième tentative donne à la probabilité
-ième tentative donne à la probabilité ![]() de la présence des clés sous ce
de la présence des clés sous ce ![]() -ième lampadaire une valeur plus grande que celle qu’elle avait a priori au départ :
-ième lampadaire une valeur plus grande que celle qu’elle avait a priori au départ :
![]()
![]()
Ce calcul montre en particulier que pour ![]() :
:
![]()
et donc que cette probabilité est maximale lorsque le quotient
Ceci conduit au second paradoxe du lampadaire : la probabilité de trouver ses clés après une succession d’échecs peut être plus grande sous un lampadaire autre que le premier, même si ce dernier était a priori le plus probable… Par exemple :
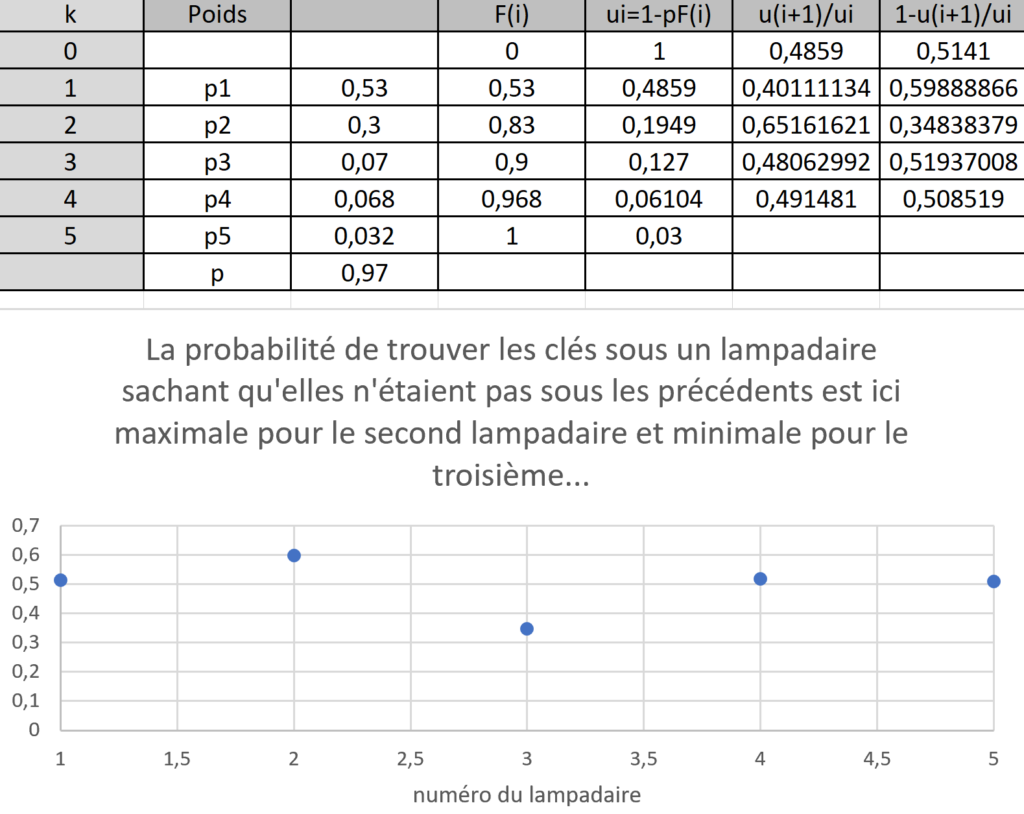
L’histoire est intéressante, car elle permet de décrire la ténacité de quelqu’un qui s’accroche échec après échec en poursuivant son effort. Dans cette description, la forme de la distribution de la probabilité ![]() est importante. Si, par exemple, l’individu n’a aucune idée de l’endroit où il a perdu ses clés, il peut supposer les lampadaires équiprobables : pour tout lampadaire
est importante. Si, par exemple, l’individu n’a aucune idée de l’endroit où il a perdu ses clés, il peut supposer les lampadaires équiprobables : pour tout lampadaire ![]() dans {1,2,…,n} :
dans {1,2,…,n} : ![]() .
.
Dans ce cas, la persévérance de l’individu repose beaucoup sur l’espoir de trouver la clé sous un des lampadaires non encore explorés. Après ![]() échecs, cette probabilité s’écrit avec l’hypothèse d’équiprobabilité des lampadaires :
échecs, cette probabilité s’écrit avec l’hypothèse d’équiprobabilité des lampadaires :
![]()
Question : Parmi toutes les distributions ![]() possibles, la distribution équiprobable
possibles, la distribution équiprobable ![]() est-elle optimale au sens où pour tout
est-elle optimale au sens où pour tout ![]() dans
dans ![]() :
:
![]()